矩阵变化的关键在于找到变换后向量坐标与变换前的关系
2D Transform 二维变换 #
Scale 缩放 #
Scale Matrix 缩放矩阵 #
Reflection Matrix 翻转矩阵 #
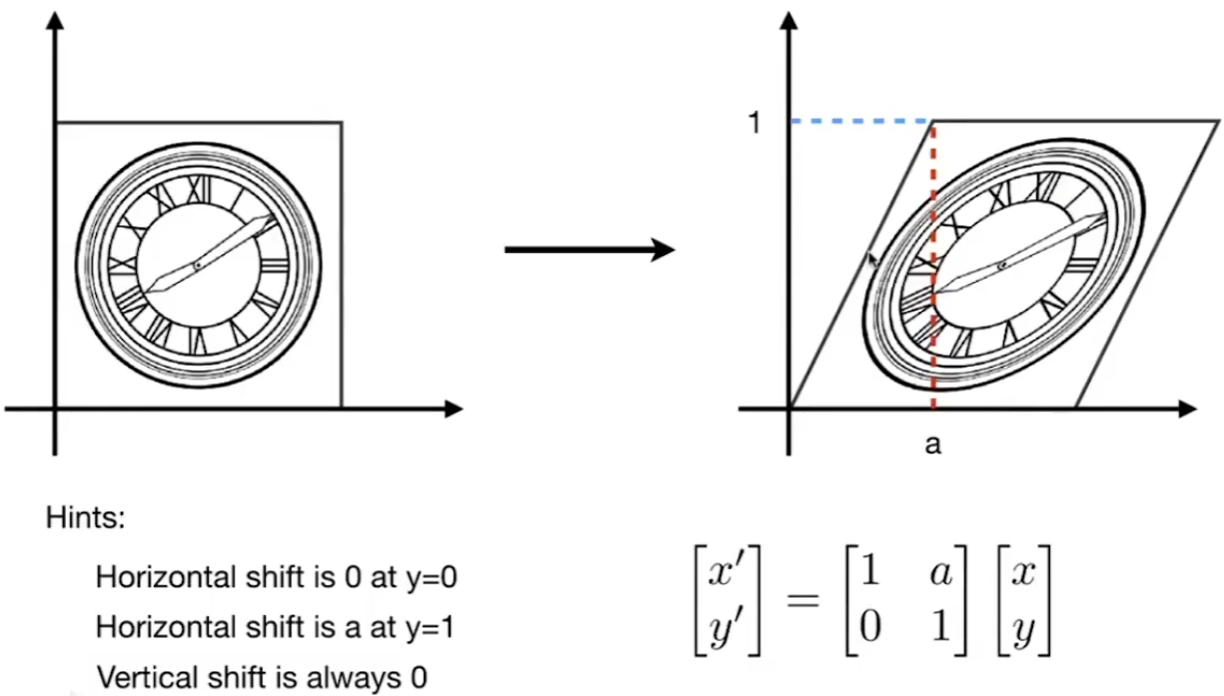
Shear Matrix 切变矩阵 #
Rotate 旋转 #
课程中默认情况的旋转讨论以 (0, 0) 为中心逆时针旋转
Rotation Matrix 旋转矩阵 #
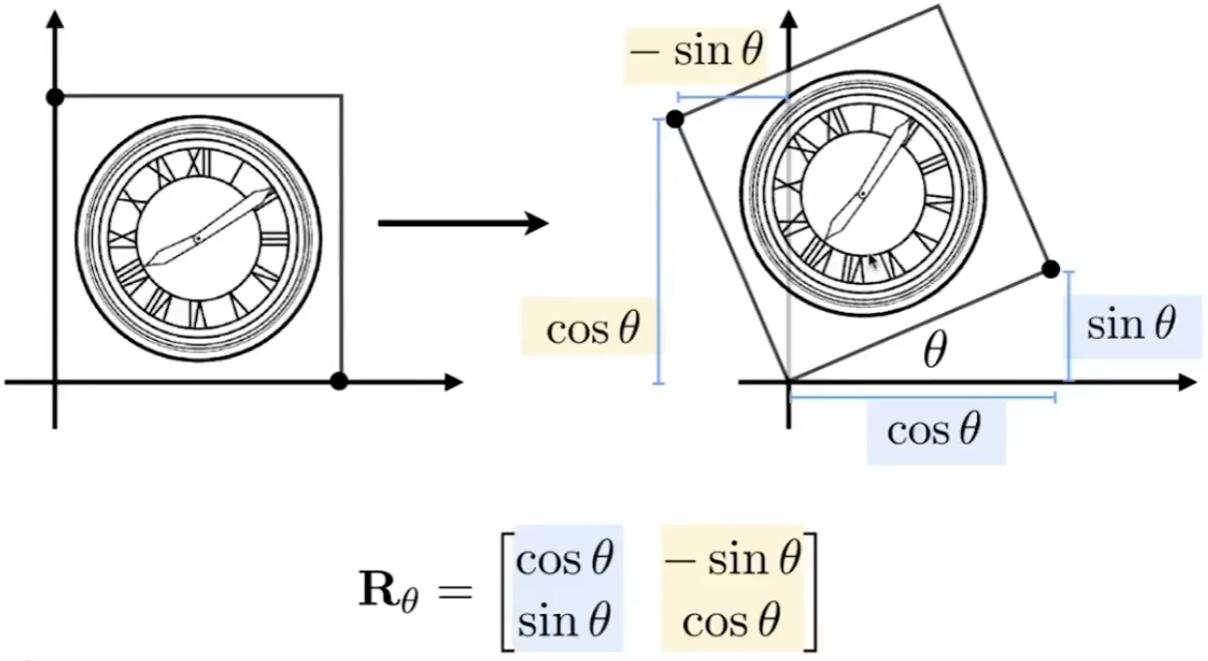
旋转矩阵的推导(基于二维平面的讨论) #
被变换的形状所有点都进行同样的变换,从特殊点 A (1, 0) 进行推导,A 旋转后可以在坐标系中构建直角三角形,根据三角函数可得 \(A^\prime(\cos\theta, \sin\theta)\) 把变化矩阵考虑成四个未知数可以得到如下等式 $$ \begin{pmatrix} \cos\theta\newline \sin\theta \end{pmatrix}= \begin{pmatrix} A & B\newline C & D \end{pmatrix} \begin{pmatrix} 1\newline 0 \end{pmatrix} $$ 经过行列式计算可得 \(A = \cos\theta, B = \sin\theta\) 对于 C,D 可以以特殊点 B (0, 1) 进行同样的推导
Linear Transforms = Matrices 线性变换即矩阵 #
相同维度的矩阵和向量对于任意变换都可以写成如下的线性组合 $$ x^\prime = ax + by\newline y^\prime = cx + dy $$ 从矩阵的角度看就是 $$ \begin{bmatrix} x^\prime\newline y^\prime \end{bmatrix}= \begin{bmatrix} a & b\newline c & d \end{bmatrix} \begin{bmatrix} x\newline y \end{bmatrix}=> x^\prime = Mx $$
Translation 平移 #
Homogeneous coordinates 齐次坐标 #
引入齐次坐标来统一所有的变换形式。在二维的空间中加入第三个坐标 $$ 2D 点 = (x, y, 1)^T\newline 2D 向量 = (x, y, 0)^T $$ 在这种情况下尝试用矩阵的形式表达变换可以得到如下的式子,对于向量来说,向量的基本性质要求向量具有平移不变的性质,因此向量引入的第三个坐标是 0 可以保护向量经过同样的运算后不会发生变化
$$ \begin{pmatrix} x^\prime\newline y^\prime\newline w^\prime \end{pmatrix}= \begin{pmatrix} 1 & 0 & t_x\newline 0 & 1 & t_y\newline 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} x\newline y\newline 1 \end{pmatrix} = \begin{pmatrix} x + t_x\newline y + t_y\newline 1 \end{pmatrix} $$ 进一步考虑引入第三个坐标后向量和点之间的加减运算,可以很容易想出,第三个坐标的变化同时反映了运算后的结果,例如点减去点,横纵坐标各自减去后,第三个坐标是 1 - 1 = 0 反映出点减点得到向量的性质,考虑点加点的运算会使第三个坐标等于 2,因此使用一种新定义来更好的描述齐次坐标中的点
在其次坐标系中 \(\begin{pmatrix}x\newline y\newline w\end{pmatrix}\) 是一个 2D 的点 \(\begin{pmatrix}x/w\newline y/w\newline 1\end{pmatrix}, w \ne 0\)
因此点加点最后得到的是两个点的中点
Affine Transformations 仿射变换 #
对于形如下图的变换称之为仿射变换,理解为 仿射变换映射 = 线性变换映射 + 平移变换
$$
\begin{pmatrix}
x^\prime\newline
y^\prime
\end{pmatrix}=
\begin{pmatrix}
a & b\newline
c & d
\end{pmatrix}\cdot
\begin{pmatrix}
x\newline
y
\end{pmatrix} +
\begin{pmatrix}
t_x\newline
t_y
\end{pmatrix}
$$
所有的仿射变换都可以写成齐次坐标的形式
$$
\begin{pmatrix}
x^\prime\newline
y^\prime\newline
1
\end{pmatrix}=
\begin{pmatrix}
a & b & t_x\newline
c & d & t_y\newline
0 & 0 & 1
\end{pmatrix}\cdot
\begin{pmatrix}
x\newline
y\newline
1
\end{pmatrix}
$$
Inverse Transform 逆变换 #
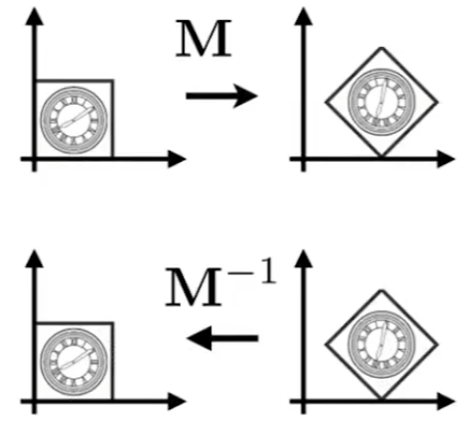
所有的变换矩阵都可以用它的逆矩阵恢复变换前的状态,从数学的角度来看,矩阵乘以变换矩阵再乘以变换矩阵的逆矩阵等于矩阵乘以一个单位矩阵,相当于没有做任何变换
Composite Transform 复合变换 #
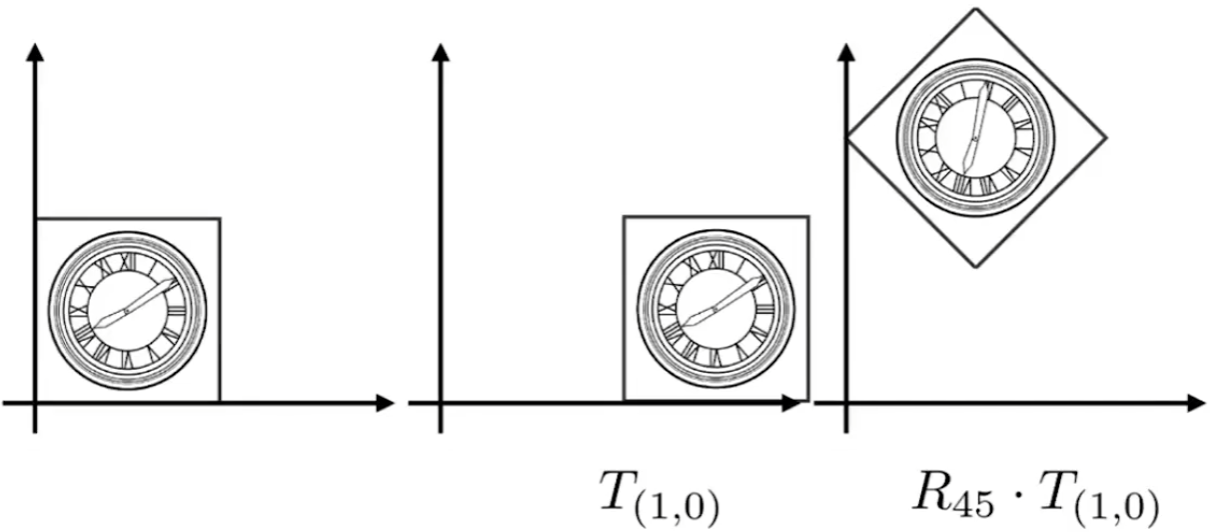
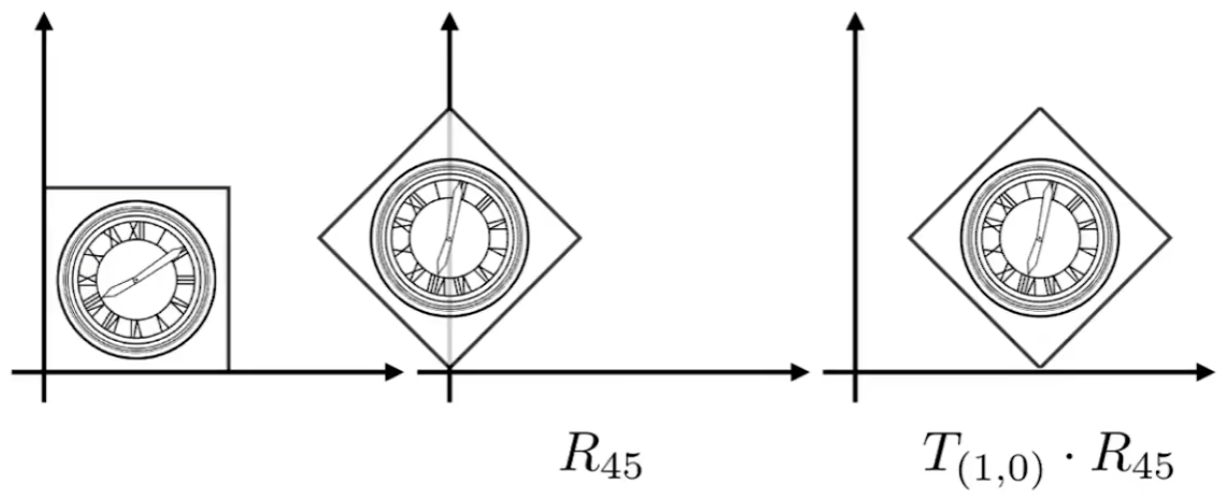
由上图可知,复杂的变换可以由基础变换得到,并且基础变换的顺序不同结果不同,这也体现了矩阵乘法不满足交换律的性质,需要注意矩阵变换是从右向左依次应用的
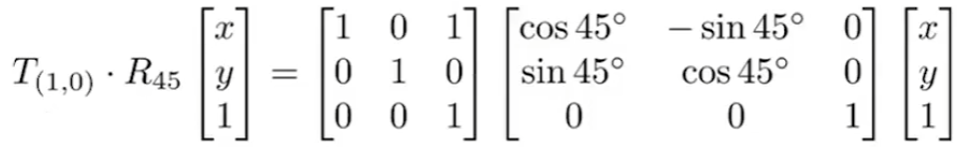
在实际的程序中,考虑到性能表现以及矩阵乘法满足结合律的特性,可以把大量的基础变换先行计算得到一个最终的变换矩阵,再应用到需要变换的矩阵上
Decomposing Complex Transforms 分解复合变换 #
考虑一种不以原点为中心的旋转变换,可以先把指定为旋转中心的点平移变换到原点,经过其它变换后再应用平移变换的逆变换

3D Transform 三维变换 #
和二维变换基本类似,也可以引入第四个坐标来完成矩阵形式的表达 $$ 3D 点 = (x, y, z, 1)^T\newline 3D 向量 = (x, y, z, 0)^T $$
在其次坐标系中 \(\begin{pmatrix}x\newline y\newline z\newline w\end{pmatrix}\) 是一个 3D 的点 \(\begin{pmatrix}x/w\newline y/w\newline z/w\newline 1\end{pmatrix}, w \ne 0\)

